In this post, we're going to get to the ball's motion and interaction.

The Problem

The paddle moves horizontally. The blocks don't move at all. The ball is the only character that moves and interacts with the other characters. The thing about the ball is that its motion and interaction can't really be separated (I think). Why? Because its interaction determines its motion and its motion determines its interaction.

To get what I mean, take a look at this:

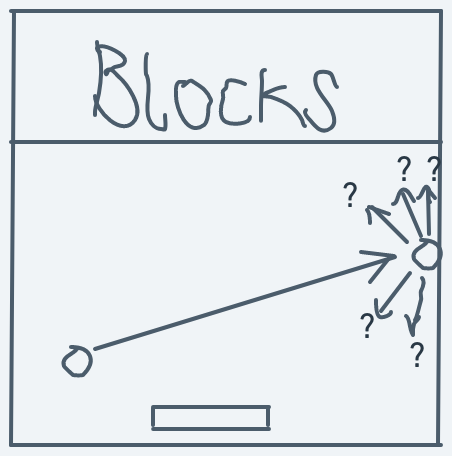
In the above image, the ball is already in motion in a northeast direction. It then hits a wall (interaction). The problem that faces us now is how we determine which direction the ball should continue motion in after this interaction.

Or, even more precisely, how do we know the ball's direction at any point in time? How can we compute the direction that the ball should change into given a pre-interaction direction and an interaction with another character?

It's only after we have precise answers to these questions that we can implement the ball's motion and interaction.

To solve the problem of simple motion, we already have our coordinate system which we looked at in the previous post. To solve the problem of direction, we have to take a little detour to look at the notion of turning.

Turning

A scenario

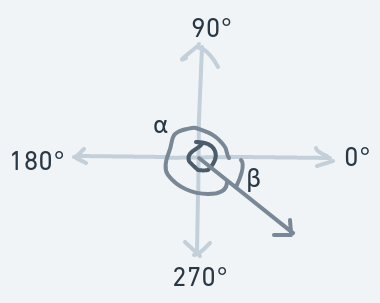
Consider a scenario: suppose you're standing on a spot and for some reason or the other, you can't leave that spot. You're facing a place; let's call this place location A. To your right is location B. Behind you is location C. To your left is location D. From an omniscient eagle's eye view, you'll look something like this:

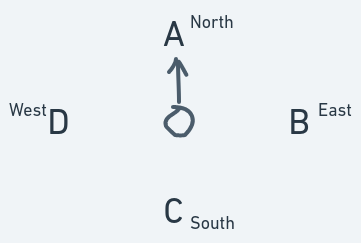
To have a reference point, we can define your current direction as north. Location B is east of you. Location C is south of you. And location D is west of you.

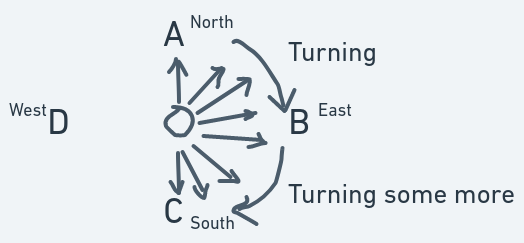
You are currently facing north. How can you face south, without moving from your spot? Well, you turn. You turn until your direction is somewhere between north and east. You keep turning until your direction becomes east. You then turn some more: your direction is between east and south. Then you make a few more turns until your direction finally becomes south.

If we were to describe the space you were standing in with a Cartesian coordinate system, like the one we settled on in the previous post, then you never changed your location. You remained in a single spot.

If you had decided to move in a straight line while you were still facing north, you would have ended up at location A. But after the turning, if you made that same straight-line motion, you would end up at location C. Why? Because that turning resulted in a change of your direction.

From this simple scenario, we can define direction as an invisible line along which a thing moves. Making this invisible line visible, we can view the change in direction like so:

How can we precisely describe the direction and changes in the direction of the ball? Saying "facing north" and "turn to the south" is insufficient. Like in the previous post, to create motion, we needed a mathematical description of space, likewise, here we need a mathematical description of direction and changes in direction.

Well, luckily for us, we don't have to invent our own descriptions of direction/turning. Mathematicians of old have already studied the notion of turning and penned down their findings. The stuff we're going to use here is from little corners in branches of math known as trigonometry and Euclidean geometry.

Angles and The Unit Circle

I'm assuming that most people would be familiar with angles, basic trig and the trig functions sine and cosine. If you aren't, please check out the references and do a bunch of Google searches. You may also consider briefing through some trig sections of a math textbook.

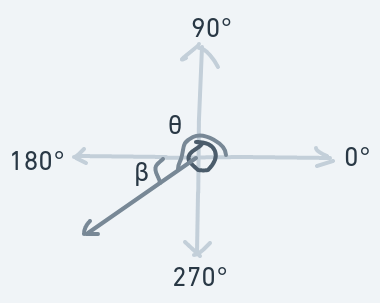
The mathematical description for a "turn" or "rotation" of an object is an angle. Consider this:

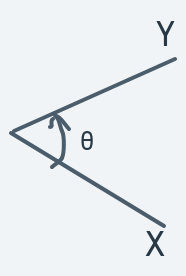
In the above diagram, the angle $\theta$ is a number that precisely says how much the line $X$ needs to be turned/rotated to become line $Y$. You can think of it as rotational distance.

Remember angles are measured in degrees (they can be measured in other units too, but we'll focus on degrees). In the scenario presented in the previous section, you turn 180 degrees to face location C.

Trig has a lot to do with the study of right-angle triangles and their properties. Remember that a right-angle triangle is a triangle in which one of the angles is a right angle (that is, 90 degrees).

For example:

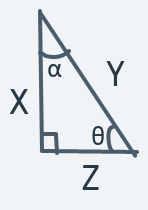
In the diagram above, the bottom left corner of the triangle is a right angle. The other angles are labeled $\alpha$ and $\theta$.

Trig functions are functions that describe a relationship between angles in a right-angle triangle and the sides of the triangle. The two that will be of use to us here are sine and cosine.

The sine of an angle in a right-angle triangle is defined as the side opposite the angle divided by the triangle's hypotenuse (the longest side). While the cosine of an angle is defined as the side adjacent to the angle divided by the hypotenuse.

For example, in the above right-angle triangle, the sine of angle $\theta$ is $(length of X) / (length of Y)$. Why? Because the side $X$ is opposite the angle $\theta$ and the side $Y$ is the longest side of the triangle (the hypotenuse). The cosine of angle $\theta$ will be $(length of Z) / (length of Y)$ because the side $Z$ is the one adjacent to angle $\theta$ and $Y$ is the longest side.

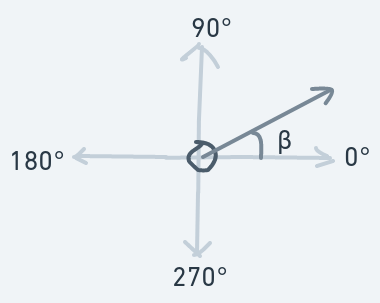
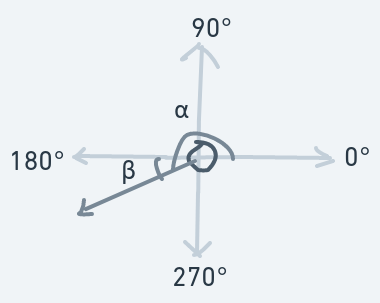
The trig functions of a right-angle triangle can also be defined on a unit circle (a circle whose radius is 1 unit):

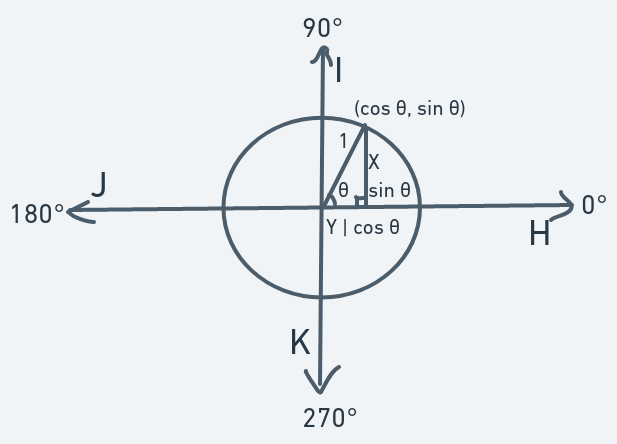
The above is a unit circle demonstrating how it can be used to compute trig functions sine and cosine of an angle labeled $\theta$.

The radius acts as the hypotenuse. The angle of concern is the angle $\theta$ which lies between the radius and the line pointing to the east. The side opposite angle $\theta$ is $\sin \theta$ because $\sin \theta = (length of X) / 1 = length of X$. The same goes for the length of the adjacent side: it is $\cos \theta$ because $\cos \theta = (length of Y) / 1 = length of Y$.

Using this definition of angles in a unit circle, we can have well-defined descriptions of direction and descriptions of changes in direction:

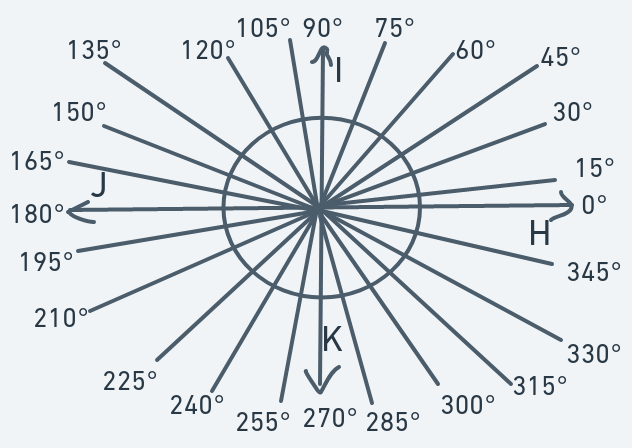
Going back to the scenario in the previous section, according to this system for defining directions, your initial direction was 90 degrees and after the turning, your final direction was 270 degrees.

With this arrangement, we have a precise description of direction. Instead of saying north, we say "90 degrees". Instead of saying "somewhere southwest", we say either "195 degrees" or "210 degrees" or "225 degrees" or "240 degrees" or "255 degrees", depending on how much towards the south or the west the direction is inclined.

A problem seems to arise here. How can we precisely determine a direction that lies between 195 and 210 degrees, since angles between those numbers are not defined in this system? Well, we don't need to. This system is already precise enough for our purposes, I believe.

That's it for defining direction. As for changing direction, all we have to do is simple arithmetic on these numbers. Going back to the previous scenario, initially, your direction is 90 degrees. To turn around, the direction is increased modulo 360. That is, it's increased from 90 to 115 to 130 to 145 to ... to 180 to ... to 270 to ... to 345 to 0 to ... to 90 degrees (full circle).

Diagonal Motion, Reflection

In the previous section, we have the answer to two of our problems: a precise description of direction and changes in direction.

The remaining problems which must be resolved before moving on: how do we determine the direction the ball ought to move in after an interaction (collision) with some other character? And how do we translate the ball's motion in a particular direction into a smooth movement on the screen (in as simple a way as possible)?

To resolve direction change after a collision, we look to another math concept: linear transformation.

We're using linear transformation here because it's simple, intuitive and direct (that is if you're already familiar with the Cartesian Coordinate system and basic trig which I assume you are). And also because the mechanisms used to effect it are just basic arithmetic.

The idea under linear transformations we'll be using to determine the ball's new direction after a collision is reflection.

When you hear the word reflection a mirror is one of the first things that may come to your mind. When you look in a mirror, you see an exact image of yourself looking right back at you. This mirror concept explains perfectly the idea of reflection.

Consider the following:

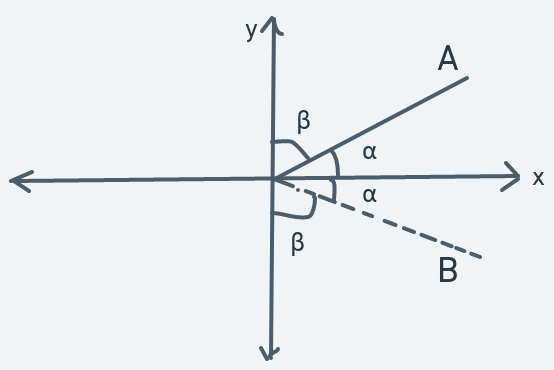
In the above diagram, if the x-axis is a mirror, the dotted line B is the image that line A will see.

Similarly:

This idea of imagining the x-axis as a mirror and drawing an identical image of some shape or line on the other side of the axis is a reflection about the x-axis.

Just like we have a reflection about the x-axis, we could also have reflections about the y-axis, too.

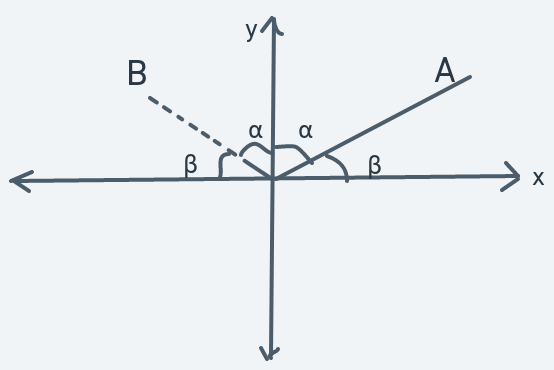
In the above diagram, if the y-axis is a mirror, then line B is what line A would see as its reflection.

Similarly:

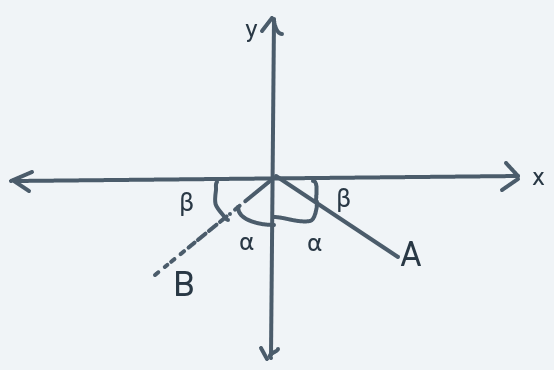
Another reflection.

Another thing to pay attention to about these reflections is the angles. When a reflection takes place, the angle between each line and the x or y axes are equal. In each reflection diagram, these equal angles are labeled with the letters $\alpha$ and $\beta$.

Using these simple ideas of reflections, we can solve the problem of determining a new direction for the ball after collision.

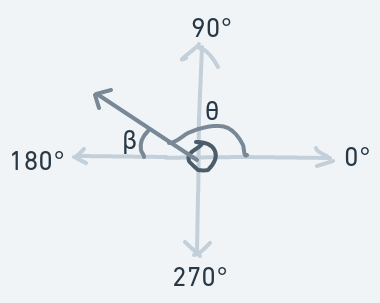
To do that, you can view direction as an invisible line along which the ball will move. For example:

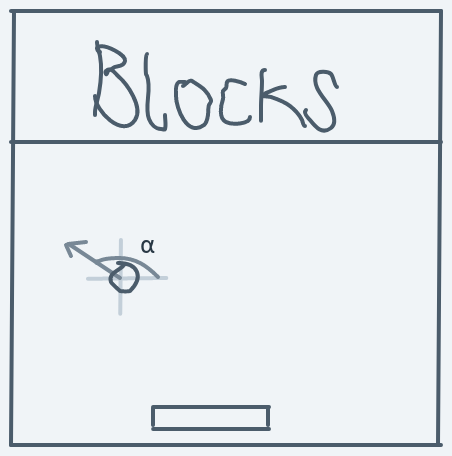
The above diagram is a snapshot of a ball in motion. The ball is moving in direction $\alpha$. The arrow is never actually seen (it's invisible). It's the representation of the ball's direction. The ball moves along that line.

How To Change Direction

Collision With The Vertical Side Of An Object

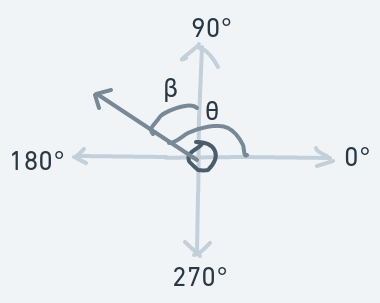
Moving Upward And Leftward (90 < Initial Direction < 180)

Now, when the ball collides with the wall, we can imagine the wall as a mirror for the invisible direction line. A reflection about the y-axis will determine the new direction for the ball.

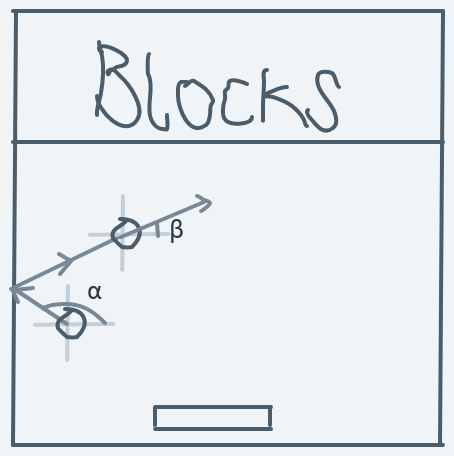
The above diagram shows how the ball's direction will change. A reflection of the ball's direction about the y-axis will serve to produce the illusion that the ball bounced off the wall.

Before collision, the ball's direction is $\alpha$:

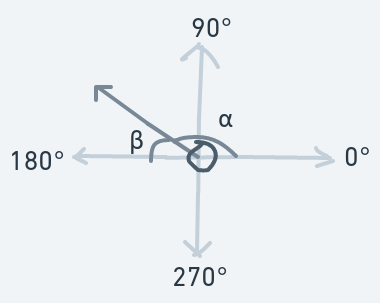
After the collision, the ball's new direction is $\beta$:

Observe that before the collision, the angle between the direction line and the x-axis is $\beta$. And after the collision $\beta$ becomes the new direction.

From our observation of this $\alpha$-$\beta$ relation, we can determine a formula that we can use anytime we need to compute a new direction after such a collision:

%% Old Direction: \alpha %% %% New Direction: \beta %% %% = 180 - \alpha %%

The direction change above is for a left wall (or any vertical object, really) collision while the ball is moving upwards and leftwards.

Moving Downward And Leftward (180 < Initial Direction < 270)

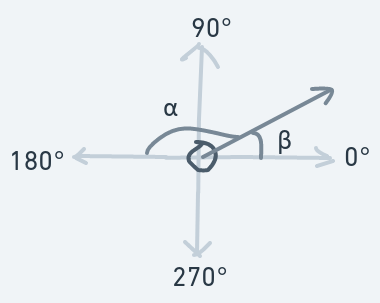
But what if the ball is moving downwards?

Before the collision:

After the collision:

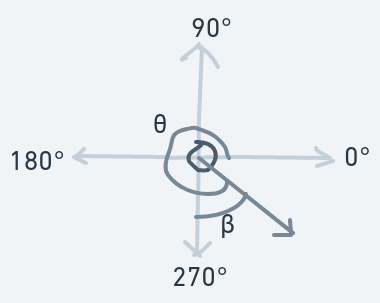
Formula for direction change:

%% Old Direction: \alpha %% %% New Direction: \theta %% %% = 270 + \beta %% %% = 270 + (270 - \alpha) %% %% = 270 + 270 - \alpha %% %% = 540 - \alpha %%

These ideas are only useful when the ball hits the vertical side of an object from the ball's left.

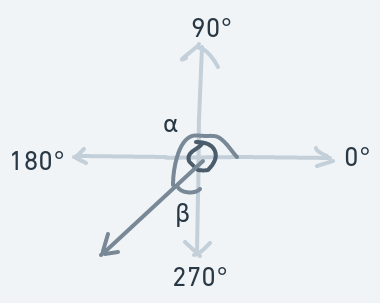
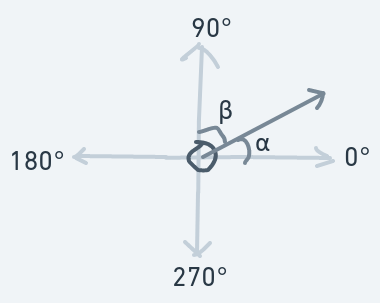
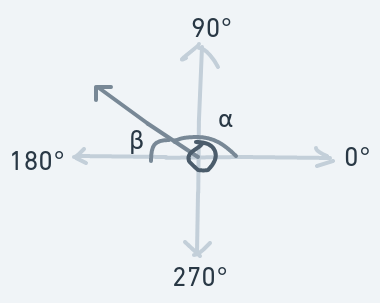
Moving Upward And Rightward (0 < Initial Direction < 90)

How about hitting from the ball's right?

The above is a diagram of the ball hitting the vertical side of an object (the right wall) from the ball's right while the ball is moving upwards.

Before the collision:

After the collision:

Formula for direction change:

%% Old Direction: \alpha %% %% New Direction: \theta %% %% = 90 + \beta %% %% = 90 + (90 - \alpha) %% %% = 90 + 90 - \alpha %% %% = 180 - \alpha %%

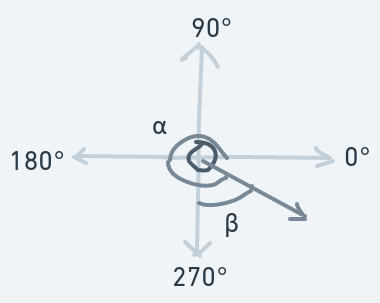
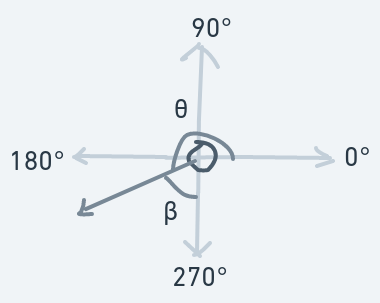
Moving Downward And Rightward (270 < Initial Direction < 360)

Now, for the ball hitting the same vertical side, but moving downwards instead of up:

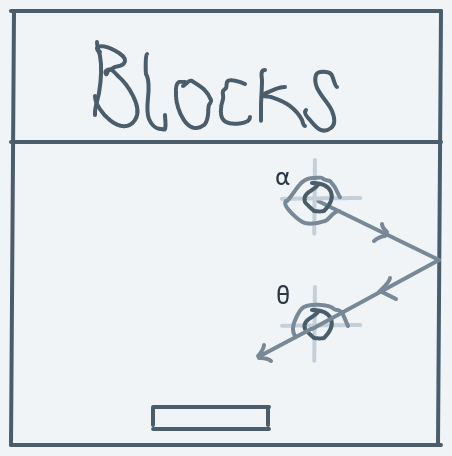
Before collision:

After collision:

Formula for direction change:

%% Old Direction: \alpha %% %% New Direction: \theta %% %% = 270 - \beta %% %% = 270 - (\alpha - 270) %% %% = 270 - \alpha + 270 %% %% = 540 - \alpha %%

These descriptions of direction changes are only for scenarios where the ball collides with the vertical side of an object.

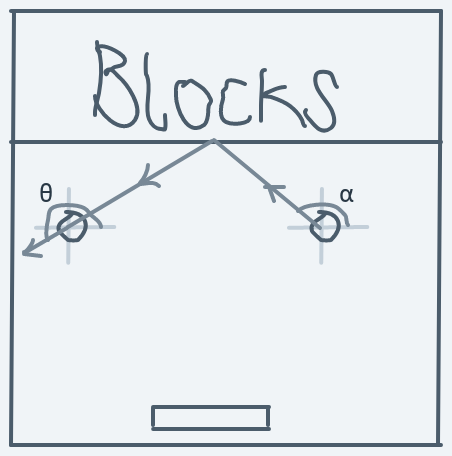
Collision With The Horizontal Side Of An Object

But what if it collides with the horizontal side (like in the case of the paddle)?

To create the illusion of the ball bouncing off walls (or a vertical side of any object), we reflect the direction about the y-axis. But to create the illusion of bouncing off the horizontal side, we reflect the direction about the x-axis instead.

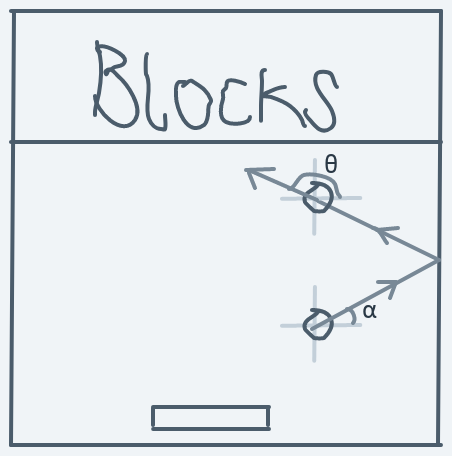
Moving Upward And Rightward (0 < Initial Direction < 90)

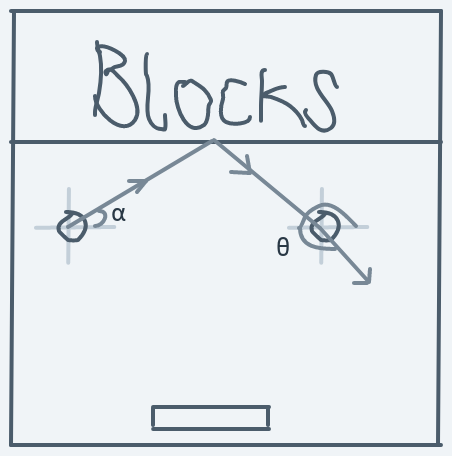
The above is a diagram of the ball hitting the horizontal side of a block while moving upwards toward the right.

Before the collision:

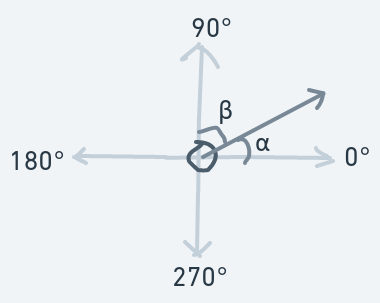
After the collision:

Formula for direction change:

%% Old Direction: \alpha %% %% New Direction: \theta %% %% = 270 + \beta %% %% = 270 + (90 - \alpha) %% %% = 270 + 90 - \alpha %% %% = 360 - \alpha %%

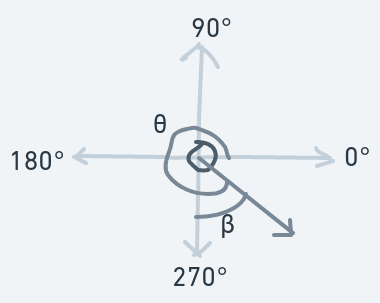
Moving Upward And Leftward (90 < Initial Direction < 180)

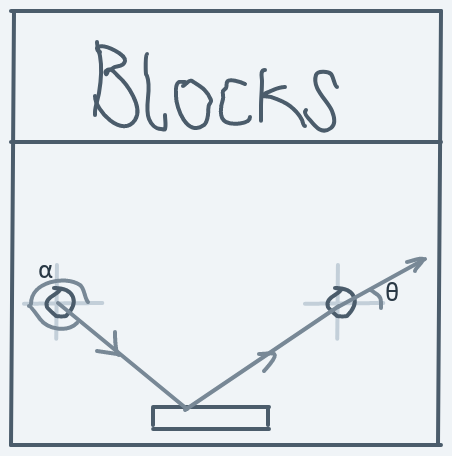
For the ball hitting the same horizontal side while moving upwards, but towards the left:

Before collision:

After collision:

Formula for direction change:

%% Old Direction: \alpha %% %% New Direction: \theta %% %% = 180 + \beta %% %% = 180 + (180 - \alpha) %% %% = 180 + 180 - \alpha %% %% = 360 - \alpha %%

Moving Downward And Rightward (270 < Initial Direction < 360)

Now, for the ball hitting a horizontal side, but moving downwards towards the right:

Before collision:

After collision:

Formula for direction change:

%% Old Direction: \alpha %% %% New Direction: \beta %% %% = 360 - \alpha %%

Moving Downward And Leftward (180 < Initial Direction < 270)

And finally for the scenario in which the ball hits a horizontal side of an object while moving downwards towards the left.

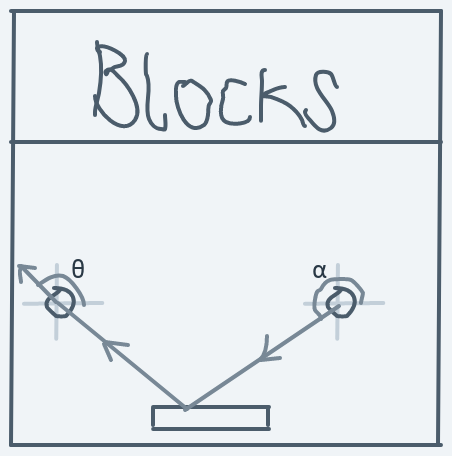
Before collision:

After collision:

Formula for direction change:

%% Old Direction: \alpha %% %% New Direction: \theta %% %% = 180 - \beta %% %% = 180 - (\alpha - 180) %% %% = 180 - \alpha + 180 %% %% = 360 - \alpha %%

Edge Cases

The descriptions above assume that the direction is always either between 0 and 90 or between 90 and 180 or between 180 and 270 or between 270 and 360. But what if it's not?

Initial Direction == 0

In this case, the ball is moving horizontally towards the right. We simply reflect it to move in the opposite direction, giving us 180 degrees.

Initial Direction == 90

In this case, the ball is moving vertically upwards. We simply reflect it to move in the opposite direction, giving us 270 degrees.

Initial Direction == 180

Here, the ball is moving horizontally toward the left. A reflection to move in the opposite direction will make the ball's new direction == 0.

Initial Direction == 270

Here, the ball is moving vertically downward. A reflection will change its direction to 90 degrees.

Summary

And with these descriptions, we have laid down the arithmetic procedures that must be performed on the ball's direction to determine its new direction after a collision in any scenario.

More compactly:

For collisions on the vertical side of objects:

For collisions on the horizontal side of objects:

For edge cases:

%% Before: \alpha %% %% After: (\alpha + 180) \ mod \ 360 %%

And that sums it up.

As for the edge cases, I think it would be a good idea to just avoid them. They're flaws in our system.

From Direction To Motion

Before we get on to implementation, we have to deal with one more problem: how do we convert the ball's direction into smooth motion on screen? To do this, let's return to the idea of the unit circle:

The radius of the circle is the direction line of direction $\theta$. When the ball's direction is $\theta$, it moves along this diagonal line.

In the previous post, we saw how to make an object move diagonally. It's a simple matter of increasing the x and y coordinates by some amount. To translate direction in the unit circle diagram to motion, we can interpret $\sin \theta$ to mean the amount by which the y coordinate should be changed to move along the direction line and $\cos \theta$ to mean the amount by which the x coordinate should be changed to move along the direction line.

We can then redefine $\sin \theta$ and $\cos \theta$ for all possible direction values in the system to have values that can believably effect this interpretation.

For example, if we define $\sin \theta = 3$ and $\cos \theta = 3$ for some direction $\theta$, then moving in that direction will go like this:

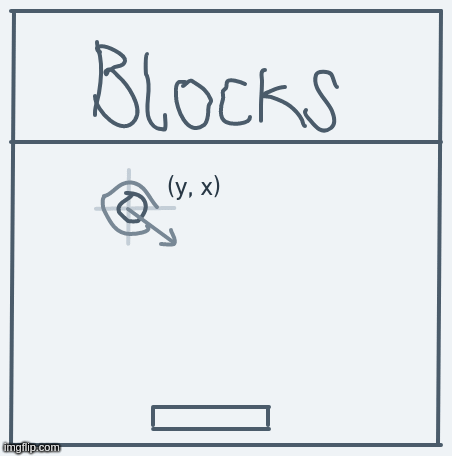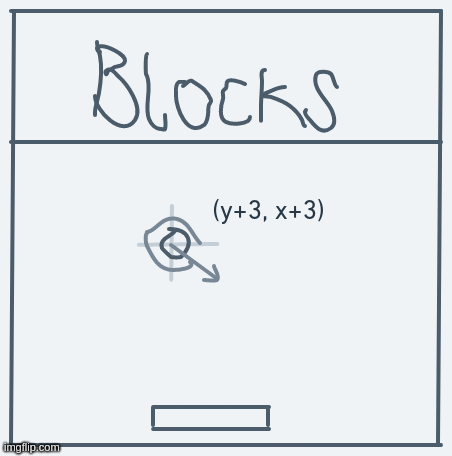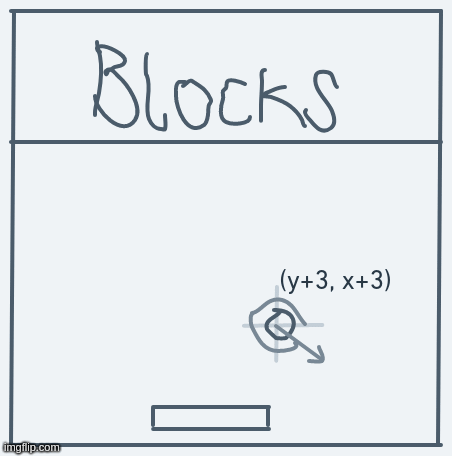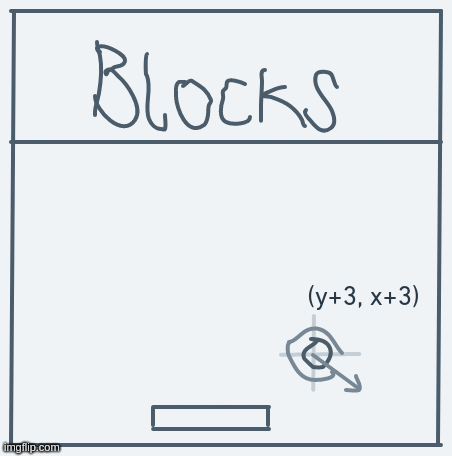
With this interpretation, the only work we'll have to do to get the system to work is to define values for $\sin \theta$ and $\cos \theta$ for each possible $\theta$ value.

In our system, $\sin \theta$ is no longer $(Opposite Side) / (Longest Side)$ and $\cos \theta$ is no longer $(Adjacent Side) / (Longest Side)$.

So, if the ball is at point (y, x) and its direction is $\theta$, then the next point it ought to move to will be (y + $\sin \theta$, x + $\cos \theta$).

Redefinitions of $\sin \theta$ and $\cos \theta$

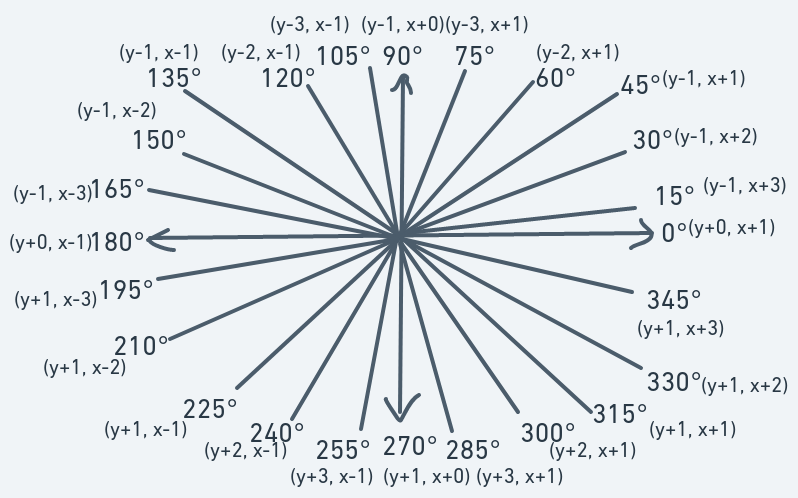
Now, we have to redefine $\sin \theta$ and $\cos \theta$ for degree values 0, 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, 270, 285, 300, 315, 330, and 345.

$\theta = 0$

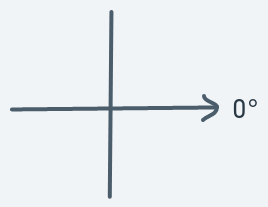This is one of those edge cases that should be avoided. Here, the direction is completely toward the right, there is no upward or downward component. So the result should be a pure horizontal motion.

It points towards the right, so it should result in a motion to the right.

We now put down definitions as follows:

%% \sin 0 = 0 %% %% \cos 0 = 1 %%

Meaning if the object at point (y, x) has a direction of 0, then the next point to move to should be (y + 0, x + 1) = (y, x + 1).

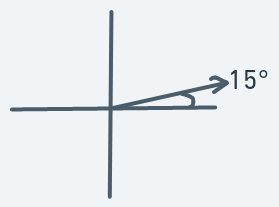An object moving in this direction should result in a significant motion to the right and a slight motion upward.

Definitions (randomly chosen as what just felt right to me):

%% \sin 15 = -1 %% %% \cos 15 = 3 %%

Remember that in our game's coordinate system, going upwards requires a reduction in the y coordinate. That's why $\sin 15$ is defined as a negative number.

This definition means that if an object is at point (y, x) and has a direction of 15, then the next point to move to should be (y - 1, x + 3).

$\theta = 30$

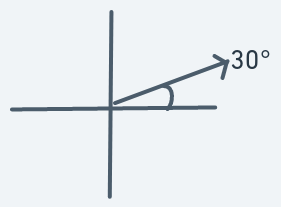An object moving in this direction should have a motion similar to that in direction 15 degrees, but the ascent should be sharper.

Definitions:

%% \sin 30 = -1 %% %% \cos 30 = 2 %%

Meaning if the object at (y, x) has a direction of 30, then the next point to move to will be (y - 1, x + 2).

$\theta = 45$

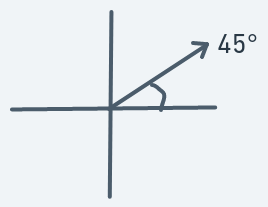Again, an object moving in this direction should have a motion similar to that in 15 degrees, but the ascent should be sharper giving the impression that the ball is moving upward at a higher degree.

Definitions:

%% \sin 45 = -1 %% %% \cos 45 = 1 %%

Meaning if the object at (y, x) has a direction of 45, then the next point to move to will be (y - 1, x + 1).

$\theta = 60$

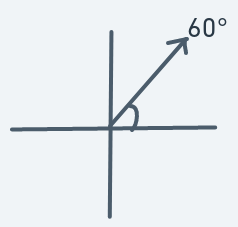Similar to 45 degrees motion. Sharper ascent.

Definitions:

%% \sin 60 = -2 %% %% \cos 60 = 1 %%

Meaning if the object at (y, x) has a direction of 60, then the next point to move to will be (y - 2, x + 1).

$\theta = 75$

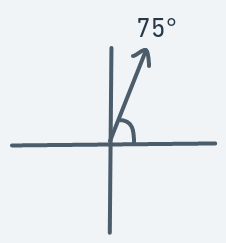Similar to 60 degrees motion. Sharper ascent.

Definitions:

%% \sin 75 = -3 %% %% \cos 75 = 1 %%

Meaning if the object at (y, x) has a direction of 75, then the next point to move to will be (y - 3, x + 1).

$\theta = 90$

Here, the direction is solely upward. There is no horizontal aspect.

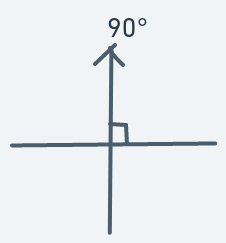
Definitions:

%% \sin 90 = -1 %% %% \cos 90 = 0 %%

Meaning if an object at (y, x) has a direction of 90, then the next point to move to will be (y - 1, x + 0).

$\theta = 105$

An object moving in this direction should have a significant motion upward and a slight one to the left.

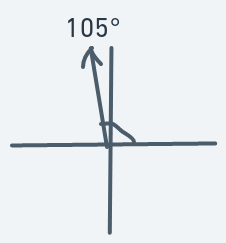
Definitions:

%% \sin 105 = -3 %% %% \cos 105 = -1 %%

Meaning an object at (y, x) has a direction of 105, then the next point to move to will be (y - 3, x - 1).

$\theta = 120$

Similar to 105 degrees motion. Duller ascent.

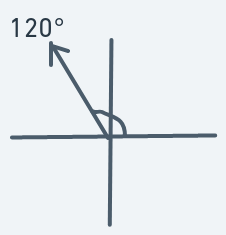
Definitions:

%% \sin 120 = -2 %% %% \cos 120 = -1 %%

Meaning if an object is at (y, x) with direction 120, then the next point to move to will be (y - 2, x - 1).

$\theta = 135$

Similar to 120 degrees motion. Duller ascent.

Definitions:

%% \sin 135 = -1 %% %% \cos 135 = -1 %%

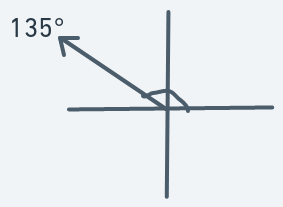
Meaning if an object is at (y, x) with direction 135, then the next point to move to will be (y - 1, x - 1).

$\theta = 150$

An object moving in this direction should move more horizontally than vertically, but not too much.

Definitions:

%% \sin 150 = -1 %% %% \cos 150 = -2 %%

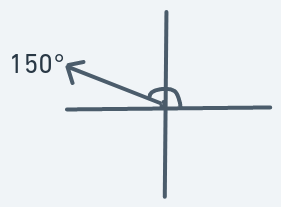
Meaning that if an object is at (y, x) with direction 150, then the next point to move to will be (y - 1, x - 2).

$\theta = 165$

Similar to 150 degrees motion. Sharper motion to the left.

Definitions:

%% \sin 165 = -1 %% %% \cos 165 = -3 %%

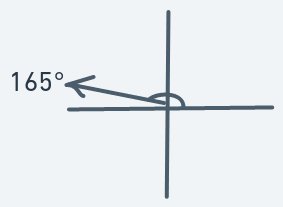
Meaning that if an object is at (y, x) with direction 165, then the next point to move to will be (y - 1, x - 3).

$\theta = 180$

Here, the direction is solely leftward. No vertical aspect.

Definitions:

%% \sin 180 = 0 %% %% \cos 180 = -1 %%

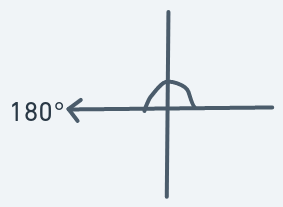
Meaning that if an object is at (y, x) with direction 180, then the next point to move to will be (y + 0, x - 1) == (y, x - 1)

$\theta = 195$

An object moving in this direction should move significantly to the left and slightly downward.

Definitions:

%% \sin 195 = 1 %% %% \cos 195 = -3 %%

Remember that in our coordinate system, a positive increase in the y coordinate results in a downward movement. That's why the $\sin$ value is positive.

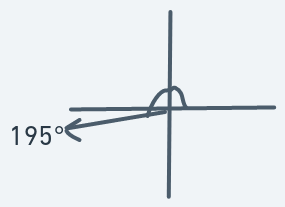
This definition means that if an object is at (y, x) with direction 195, then the next point to will be (y + 1, x - 3).

$\theta = 210$

Similar to 195 degrees motion. Duller leftward motion.

Definitions:

%% \sin 210 = 1 %% %% \cos 210 = -2 %%

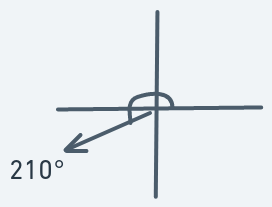
Meaning that if an object is at (y, x) with direction 210, then the next point to move to will be (y + 1, x - 2).

$\theta = 225$

Similar to 210 degrees motion. Duller leftward motion.

Definitions:

%% \sin 225 = 1 %% %% \cos 225 = -1 %%

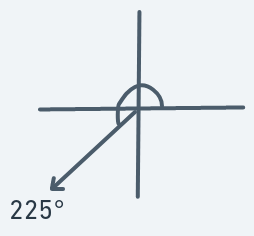
Meaning that if an object is at (y, x) with direction 225, then the next point to move to will be (y + 1, x - 1).

$\theta = 240$

An object moving in this direction should move more downward than leftward and not too much.

Definitions:

%% \sin 240 = 2 %% %% \cos 240 = -1 %%

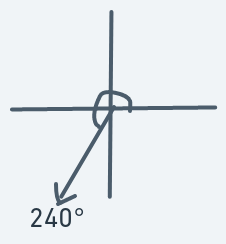
Meaning that if an object is at (y, x) with direction 240, then the next point to move to will be (y + 2, x - 1).

$\theta = 225$

Similar to 240 degrees motion. Sharper downward movement.

Definitions:

%% \sin 255 = 3 %% %% \cos 255 = -1 %%

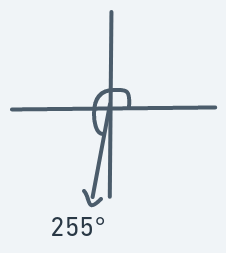
Meaning that if an object is at (y, x) with direction 255, then the next point to move to will be (y + 3, x - 1).

$\theta = 270$

No horizontal component. Just vertical downward motion.

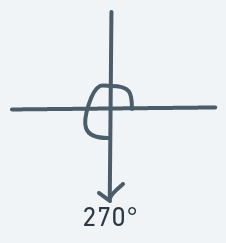
Definition:

%% \sin 270 = 1 %% %% \cos 270 = 0 %%

Meaning that if an object is at (y, x) with direction 270, then the next point to move to will be (y + 1, x + 0).

$\theta = 285$

Significant Downward motion. Slight motion to the right.

Definition:

%% \sin 285 = 3 %% %% \cos 285 = 1 %%

Meaning that if an object is at (y, x) with direction 285, then the next point to move to will be (y + 3, x + 1).

$\theta = 300$

Similar to 285 degrees motion. Duller downward motion.

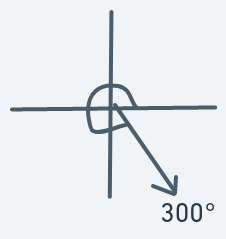
Definition:

%% \sin 300 = 2 %% %% \cos 300 = 1 %%

Meaning that if an object is at (y, x) with direction 300, then the next point to move to will be (y + 2, x + 1).

$\theta = 315$

Similar to 315 degrees motion. Duller downward motion.

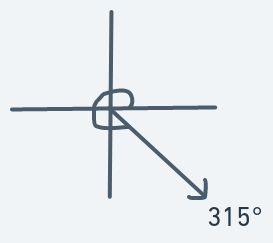
Definition:

%% \sin 315 = 1 %% %% \cos 315 = 1 %%

Meaning that if an object is at (y, x) with direction 315, then the next point to move to will be (y + 1, x + 1).

$\theta = 330$

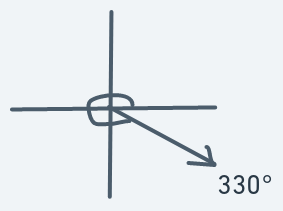Motion to the right should be more than the downward motion, but not too much.

Definitions:

%% \sin 330 = 1 %% %% \cos 330 = 2 %%

Meaning that if an object is at (y, x) with direction 330, then the next point to move to will be (y + 1, x + 2).

$\theta = 345$

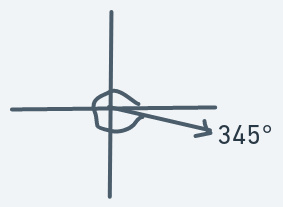Similar to 330 degrees motion. Sharper rightward motion.

Definitions:

%% \sin 345 = 1 %% %% \cos 345 = 3 %%

Meaning that if an object is at (y, x) with direction 345, then the next point to move to will be (y + 1, x + 3).

Summary

With these descriptions, we now know how to determine the way the ball should move based on its direction.

More compactly:

Why Avoid The Edge Cases

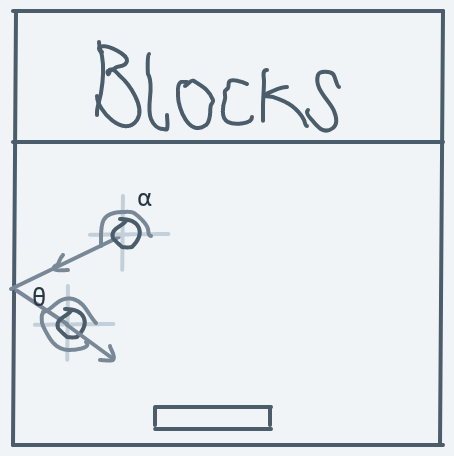
I mentioned that it would be a good idea to avoid edge cases, but why? Well, consider the following:

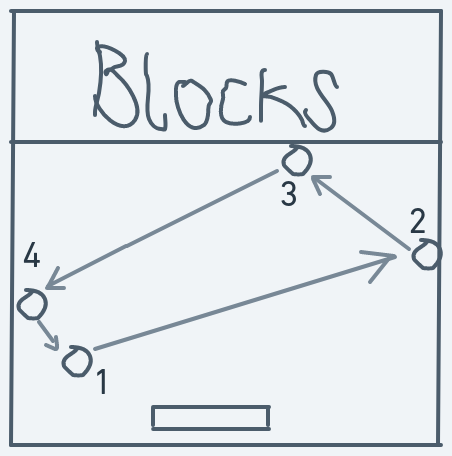
When the above ball hits the wall, it will eventually come back down in a different direction and if the human playing the game wants to win, the human will have to move the paddle to save the ball from going off-screen.

But if the ball was moving in an edge-case direction, like 90 degrees:

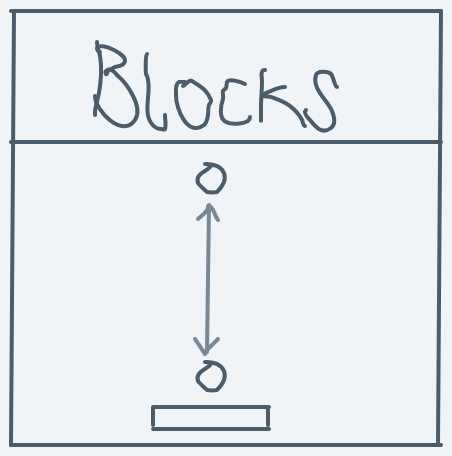
When it collides with the blocks, it will come back down in a straight line, collide with the paddle then go back up in a straight line, then collide the with blocks then come back down in a straight line then collide with the paddle, and this goes on and on, forever. Or until the user gets bored and deliberately moves the paddle out of the ball's path to lose the game.

That's horrible.

Although, there are ways these flaws could be patched. We could redefine the edge case $\sin$ and $\cos$ definitions to reflect the ball in such a way as to avoid this deadlock motion. But I'll just leave it as it is and avoid the edge cases.

Expressing The System In Code

To express our system in code, create a new file math.rs.

First, we create a structure to represent a point:

#[derive(Clone, Copy)]
pub struct Point(pub isize, pub isize);

And endow it with meaningful functions:

impl Point {
    pub fn x(&self) -> isize {
        self.1
    }

    pub fn y(&self) -> isize {
        self.0
    }

    pub fn set_x(&mut self, x: isize) {
        self.1 = x;
    }

    pub fn set_y(&mut self, y: isize) {
        self.0 = y;
    }
}

We can use this Point structure instead of littering code with tuples here and there.

For ease of use, we can also implement some traits:

impl core::ops::Add for Point {
    type Output = Point;
    fn add(self, rhs: Self) -> Self::Output {
        Self(self.0 + rhs.0, self.1 + rhs.1)
    }
}

impl core::ops::Sub for Point {
    type Output = Point;
    fn sub(self, rhs: Self) -> Self::Output {
        Self(self.0 - rhs.0, self.1 - rhs.1)
    }
}

impl core::ops::AddAssign for Point {
    fn add_assign(&mut self, rhs: Self) {
        self.0 += rhs.0;
        self.1 += rhs.1
    }
}

impl core::ops::SubAssign for Point {
    fn sub_assign(&mut self, rhs: Self) {
        self.0 -= rhs.0;
        self.1 -= rhs.1;
    }
}

With these trait implementations, we can add and subtract points as if they're regular primitives. The core::ops::Add implementation allows us to do:

let p1 = Point(5, 2);
let p2 = p1 + Point(7, 2); // Equals Point(12, 4)

The core::ops::Sub implementation allows us to do:

let p1 = Point(5, 2);
let p2 = p1 - Point(5, 2); // Equals Point(0, 0)

The core::ops::AddAssign implementation allows us to do:

let mut p1 = Point(5, 2);
p1 += Point(5, 2); // p1 is now Point(12, 4)

And the core::ops::SubAssign implementation allows us to do:

let mut p1 = Point(5, 2);
p1 -= Point(5, 2); // p1 is now Point(0, 0)

A structure to represent angles:

#[derive(Clone, Copy)]
pub struct Angle(usize);

We can impose a constraint on the usize contained so that it will always be a valid angle in the system (0, 15, 30, 45, 90, ..., 180, 195, 210, ..., 330, 345).

To do this, we leave the field private (so it can't just be changed to an invalid value elsewhere) and provide a new function that accepts a number and converts it to a valid degree.

The structure can then offer methods to manipulate the contained usize in such a way as to ensure it remains a valid degree value.

We don't have to worry about negative values because usizes can never be negative.

impl Angle {
    // Creates a new angle guaranteed to have a valid degree value in the system
    pub fn new(n: usize) -> Self {
        // Should be wrapped around
        let n = n % 360;
        // And rounded to the nearest defined angle
        let n = n - (n % 15);
        Self(n)
    }
}

To take care of given numbers greater than 360, we wrap them around with % 360. The let n = n - (n % 15) rounds the number down to the nearest multiple of 15. This results in a valid system degree because all the valid degrees are lesser than 360 and are multiples of 15.

To express the ideas of how to change direction after collisions:

pub enum SideCollided {
    Vertical,
    Horizontal
}

impl Angle {
    pub fn reflect(self, side_collided: SideCollided) -> Self {
        match self.0 {
            // Edge cases
            0 => Self(180),
            90 => Self(270),
            180 => Self(0),
            270 => Self(90),
            _ => match side_collided {
                // Collision with the verical side of an object
                SideCollided::Vertical => match self.0 {
                    0..=180 => Self(180 - self.0),
                    _ => Self(540 - self.0)
                },
                // Collision with the horizontal side of an object
                SideCollided::Horizontal => Self(360 - self.0)
            }
        }
    }
}

And for our $sines$ and $cosines$:

impl Angle {
    pub fn sin(&self) -> isize {
        match self.0 {
            0 => 0,
            15 => -1,
            30 => -1,
            45 => -1,
            60 => -2,
            75 => -3,
            90 => -1,
            105 => -3,
            120 => -2,
            135 => -1,
            150 => -1,
            165 => -1,
            180 => -1,
            195 => 1,
            210 => 1,
            225 => 1,
            240 => 2,
            255 => 3,
            270 => 1,
            285 => 3,
            300 => 2,
            315 => 1,
            330 => 1,
            345 => 1,
            // The number self.0 is guaranteed to always be a valid degree
            _ => unreachable!()
        }
    }

    pub fn cos(&self) -> isize {
        match self.0 {
            0 => 1,
            15 => 3,
            30 => 2,
            45 => 1,
            60 => 1,
            75 => 1,
            90 => 0,
            105 => -1,
            120 => -1,
            135 => -1,
            150 => -2,
            165 => -3,
            180 => 0,
            195 => -3,
            210 => -2,
            225 => -1,
            240 => -1,
            255 => -1,
            270 => 0,
            285 => 1,
            300 => 1,
            315 => 1,
            330 => 2,
            345 => 3,
            // The number self.0 is guaranteed to always be a valid degree
            _ => unreachable!()
        }
    }
}

In main.rs:

// ...Others

mod machine;
mod alloc;
mod display;
mod event_hook;
mod game;
mod sync;
mod math; // NEW

Take Away

• Direction is the invisible line along with the ball will move.
• Consider the definitions of trig functions in a unit circle; if the direction line is the 1-unit radius in that unit circle, then the represented angle is the unique identifier of the direction.
• Changing direction is by simple addition and subtraction of the direction's angle representation modulo 360.
• $\sin \theta$ is the amount by which the y coordinate should be changed to move in direction $\theta$.
• $\cos \theta$ is the amount by which the x coordinate should be changed to move in direction $\theta$.
• If the ball is at point (y, x) and has a direction of $\theta$, then the next point to move to will be $(y + \sin \theta, x + \cos \theta)$.
• Direction definitions and motions translations:

• Direction change after collisions:

For collisions on the vertical side of objects:

For collisions on the horizontal side of objects:

In The Next Post

We'll be using the system described here to implement the ball's motion and interaction.

References

• Trig: https://www.cuemath.com/trigonometry/
• Angles: https://en.wikipedia.org/wiki/Angle
• Right Angle: https://en.wikipedia.org/wiki/Right_angle
• Right Angle: https://www.cuemath.com/geometry/right-angle/
• Trig Functions: https://www.cuemath.com/trigonometry/trigonometric-functions/
• Sine and Cosine in a Unit Circle: https://math.libretexts.org/Bookshelves/Precalculus/Precalculus_1e_(OpenStax)/05%3A_Trigonometric_Functions/5.02%3A_Unit_Circle_-_Sine_and_Cosine_Functions
• Unit Circle: https://www.mathsisfun.com/geometry/unit-circle.html
• Reflection: https://www.varsitytutors.com/hotmath/hotmath_help/topics/reflections